Energy Changes In Physical And Chemical Processes
Energy is the ability to do work.
There are many forms of energy such as chemical, electrical, heat, kinetic and potential energy. Energy can neither be created nor destroyed but can only be converted from one form to another.
Endothermic and Exothermic reactions
When ammonium nitrate is dissolved in water, the temperature of the resulting solution drops. This is because heat is absorbed in the process of dissolving. This is an endothermic reaction since heat enters the system.
Endothermic reaction is a reaction that is accompanied by absorption of heat.
When sodium hydroxide dissolves in water, the temperature of the resulting solution rises. This is because heat is given out in the process. This is an Exothermic reaction due to exit of heat from the system.
Exothermic reaction is a reaction that is accompanied by production of heat.
Energy Level Diagrams
Dissolution of either sodium hydroxide or ammonium nitrate in water demonstrates that either energy is added to or lost from the system.
When energy is added to the system i.e endothermic reaction, the products are higher in energy compared to the reactants. This is illustrated using the energy level diagram below.
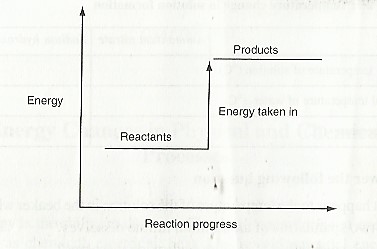
In the case where energy is lost from the system .i.e., exothermic reaction, the products have lower energy compared to reactants. This is illustrated as:
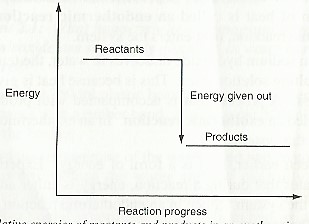
The following are elaborate diagrams for ammonium nitrate and sodium hydroxide dissolving in water respectively.

Enthalpy Notation
The heat content in a chemical is called its enthalpy. It is assigned the symbol H. It is not possible to experimentally measure it. However, a change in the heat content (enthalpy) can be easily measured since it results in a temperature change. A change in heat content (enthalpy change) is denoted by the symbol ∆H. The enthalpy change during a reaction is given by the expression:
Enthalpy change (∆H) = Enthalpy of products − Enthalpy of reactants.
In an endothermic reaction, the enthalpy of products is higher than that of the reactants. The enthalpy change is therefore positive.
In an exothermic reaction the products have lower enthalpy compared to the reactants. The enthalpy change is therefore negative. The energy change associated with a chemical change is usually shown at the end of the balanced chemical equation. E.g.
CH4(g) + 202(g) → CO2(g) + 2H2O(g) ∆H = —728 KJ.
NaNO3(s) + (aq) → NaNO3(aq) ∆H = + 21 KJ.
Bond breaking and Bond formation in Physical and Chemical Processes
Matter exists in three states namely solid, liquid and gas. When the physical conditions are changed, the states change.
Energy changes that take place when solids and liquids are heated to melting point and boiling point respectively
When ice is heated, its temperature rises as the molecules absorb heat energy. The heat energy absorbed is converted to kinetic energy. As a result, the molecules vibrate more vigorously. Eventually, the molecules gain enough kinetic energy to overcome the forces holding them together in solid. At this point, the molecules can change their positions, and the ice melts. The temperature remains constant until all the ice has melted.
The heat energy supplied during melting is used to overcome the forces holding the lattice together. It does not, therefore, result in temperature rise. The molecules have now greater freedom of movement in the liquid state.
Latent heat of fusion refers to the amount of heat energy required to convert a given amount of a solid substance into a liquid at its melting point. Latent means hidden.
Molar heat of fusion is the amount of heat energy required to convert one mole of a solid substance at its melting point into a liquid. The same amount of energy’ is liberated in the reverse process when one mole of the liquid substance at its freezing point turns into a solid.
When a liquid is heated, its temperature rises as the molecules absorb heat energy. The heat energy absorbed by the molecules is converted into kinetic energy. The vibratory motion of the molecules increases further. The temperature continues rising until the liquid begins to boil. At the boiling point, the molecules have acquired enough kinetic energy to break away from each other completely. The temperature remains constant at the boiling point because the heat energy supplied is used to break up the forces of attraction between the molecules.
Latent heat of vaporisation is the heat absorbed by a substance when changing from the liquid stale into the gaseous state at a constant temperature.
Molar heat of vaporisation refers to the heat absorbed by one mole of a substance for it to change from the liquid to the gaseous state at a constant temperature.
Molar heat of fusion and molar heat of vaporisation of a substance can be used to estimate the strength of the intermolecular forces holding the particles together in the solid and in the liquid states respectively. If the forces holding the particles together in the solid structure are strong, then the molar heat of fusion is high. This is reflected in the high melting point of the substance. Similarly, when the forces holding the particles in the liquid are strong, the molar heat of vaporisation is high. This is reflected in the high boiling point of the substance.
Table 1: shows the molar heats of fusion and vaporisation for water and ethanol
Compound |
Molar heat of fusion |
Molar heat of vaporisation |
Melting point |
Water |
6.02 KJ mol-1 |
40.7 KJ mol-1 |
273K |
Ethanol |
2.39 KJ mol-1 |
18.7 KJ mol-1 |
188K |
Reaction of Methane and Chlorine
For a reaction to occur, the covalent bonds in both methane and chlorine must be broken to obtain separate atoms. Energy is required to break these bonds. Thus, bond breaking is an endothermic process. Once the bonds are broken, the atoms rearrange themselves and new bonds are formed in the products. In the process of bond formation, energy is given out. Therefore bond formation is an exothermic process. The energy spent in breaking the bonds in the methane and chlorine molecules is less than the energy given out when the products are formed. Overall, the reaction, therefore, gives out energy. These changes can be illustrated using the energy level diagram shown in figure 2.4.

In some reactions, more energy is spent in breaking bonds in the reactants than is given out when new bonds are formed in the reactants. In such reactions, the overall process is endothermic.
Determination of Enthalpy Changes
What are the enthalpies of solution of:
(I)Ammonium nitrate, (ii) Sodium hydroxide?
-
Enthalpy of solution of Ammonium nitrate
Ammonium nitrate dissolves in water with the absorption of heat. The change is endothermic. When 2 g of ammonium nitrate is dissolved in 100 ml distilled water, a temperature change of about 1.5°C (1.5K) is noted. The change is calculated using the formula:
Heat absorbed = Mass of solution X Specific heat capacity X Temperature change.
In this case, it is assumed that the mass of the solution is equal to that of a similar amount of water. i.e 100 g (0.1 Kg). The specific heat capacity of water is used in the calculation. Therefore:
Heat absorbed = 0.l Kg X 4.2 KJ Kg K-1 X 1.5 K = 0.63 KJ
The number of moles of ammonium nitrate is calculated from the formula:
Moles =
= = 0.025 mol
This means that when 0.025 mol of ammonium nitrate dissolves,
0.63 KJ of heat is absorbed. Therefore the enthalpy change when
1 mol of ammonium nitrate dissolves is:
= = 25.2 KJ
Thus when 1 mol of ammonium nitrate dissolves 25.2 KJ of heat is absorbed. The equation for the reaction including the enthalpy change is:
NH4NO3(s) → NH4NO3(aq) ∆H = +25.2 KJ mol-1
This value: +25.2 KJ mol-1 is called the molar heat of solution of ammonium nitrate.
Molar heat of solution: is the enthalpy that that occurs when one mole of a substance dissolves in a solvent to give an infinitely dilute solution.
A chemical equation that shows the enthalpy change is called the thermochemical equation.
-
Enthalpy of Solution of Sodium Hydroxide
Sodium hydroxide dissolves in water with the evolution of heat. A temperature rise of about 5°C is recorded when 2 g of sodium hydroxide is dissolved in 100 ml distilled water.
Heat evolved = Mass of solution X Specific heat capacity X Temperature change.
= 0.1 Kg X 4.2 KJ Kg K-1 X 5 K
= 2.1 KJ
Moles of sodium hydroxide used is given by:
Moles =
= = 0.05 mol
Therefore, 0.05 mol liberates 2.1 KJ of heat
1 mol liberates:
= = 42 KJ of heat
The thermochemical equation for this reaction is:
NaOH(s) → NaOH(aq) ∆H = —42 KJ mol-1
This (i.e. — 42 KJ mol-1) is the molar heat of solution of sodium hydroxide.
What is the Heat of Solution of Concentrated Sulphuric (VI) Acid?
Concentrated sulphuric (VI) acid dissolves in water with the evolution of heat. When 2 cm3 of concentrated sulphuric (VI) acid is dissolved in 98 cm3 of water, a temperature rise of 4.5°C is recorded
The total volume of the solution = ( 2 + 98 ) cm3 = 100 cm3
In calculations of enthalpy, the solution is assumed to have a density of 1 g cm-3.
Thus the mass of solution is given by:
Mass = Volume X Density
= 100 cm3 X 1.0 g cm-3
= 100 g (0.1 Kg)
Heat evolved = Mass of solution X Specific heat capacity X Temperature change
= 0.1 Kg X 4.2 KJ Kg K-1 X 4.5K
= 1.89 KJ
The mass of the concentrated acid is calculated from the formula
Mass = Specific density X Volume
= I .84 g cm-3 X 2 cm-3
= 3.68 g.
Thus the 2 cm-3 of concentrated sulphuric (VI) acid has a mass of 3.68g. But since the acid is 98% pure, the actual mass of sulphuric (VI) acid is given by:
Actual Mass of acid = Mass of conc. Acid X Percentage purity
= 3.68 g X
= 3.6064 g
The moles of the acid is given by:
Moles =
= = 0.0368 mol
Therefore when 0.0368 mol of sulphuric (VI) acid dissolves, 1 .89
KJ of heat is evolved. When I mole of the sulphuric (VI) acid
Dissolves, = = 51.358 KJ of heat is evolved
Thus the molar heat of solution of sulphuric (VI) acid
= —51.358 KJ mol-1
The negative sign is added to show that the process is exothermic.
The thermochemical equation is:
H2SO4(l) + (aq) → H2SO4(aq) ∆H = —51.358 KJ mol-1
The molar heats of solution obtained in experiments are usually lower than those quoted in data books. Reason:
- The heat gained by the apparatus and that lost to the surrounding is not accounted for in the calculations.
What is the enthalpy of combustion of ethanol?
The enthalpy of combustion of ethanol can be obtained using the set up below
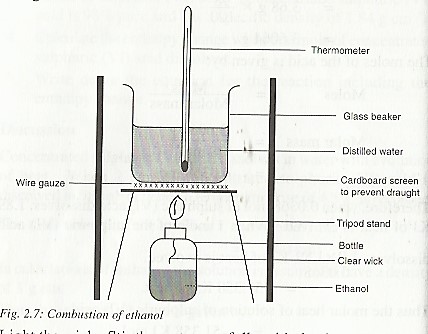
In a combustion experiment the following results were obtained:
Initial mass of bottle + its contents = 28.25 g
Final mass of bottle + its contents = 28.02 g
Mass of ethanol burnt = 0.23 g
Final temperature of water = 43.0 ᵒC
Initial temperature of water = 28.0 ᵒC
Rise in temperature of water = 15.0 ᵒC
Formula mass of ethanol, CH3CH2OH = ( 12 X 2) + 16 + 6 = 46
Moles of ethanol burned = = 0.005 mol
Heat evolved = heat gained by water
= Mass of solution X Specific heat capacity X Temperature change
= 0.1 Kg X 4.2 KJ Kg K-1 X 15 K = 6.3 KJ
Therefore 0.005 moles of ethanol liberates 6.3 KJ of heat.
Therefore 1 mol of ethanol will liberate
= = 12.60 KJ of heat is evolved
This is the molar heat of combustion of ethanol.
Molar heat of combustion: is the enthalpy change that occurs when one mole of a substance is completely burned in oxygen.
The thermochemical equation is:
CH3CH2OH(l) + 3O2(g) → 2C02(g) + H2O(l) ∆H = —1260 KJ mol-1
The enthalpy change when zinc reacts with copper (II) sulphate solution
When zinc is added to copper (II) sulphate solution an exothermic reaction occurs. The blue colour of the solution fades as brown solid is deposited. The blue colour is due to the hydrated copper (II) ions in copper (II) sulphate. During the reaction, these copper (II) ions in the solution are reduced to copper which is brown.
The zinc atoms are oxidised to zinc (II) ions which are colourless.
The equation for the reaction is:
Zn(s) + Cu2+(aq) → Zn2+(aq) + Cu(s)
The expected change in temperature for this experiment is 24.5ᵒC(24.5 K).
Moles of Zinc used = = 0.062 mol
Moles of copper (II) ions present = = 0.05 mol
Therefore the moles of zinc are in excess.
Excess zinc is used in this experiment in order to ensure that all the copper (II) ions are changed into copper metal.
Heat evolved = Mass X Specific heat capacity X Temperature change
= 0.1 Kg X 4.2 KJ Kg K-1 X 24.5 K
= 10.29 KJ
Thus when 0.05 mol of copper (II) ions are displaced from solution by zinc, 10.29 KJ of heat is evolved.
When I mol of copper (II) ion are displaced,
= 205.8 KJ of heat is evolved.
Therefore the molar heat of displacement of copper by zinc is — 205.8 KJ mol-1
Molar heat of displacement: is the enthalpy change that occurs when one mole of a substance is displaced from a solution of its ions.
The thermochemical equation for the reaction is:
Zn(s) + Cu2+(aq) → Zn2+(aq) + Cu(s) ∆H = —205.8 KJ mol-1
Heat of Neutralisalion of Hydrochloric acid by Sodium Hydroxide
During neutralization, hydrogen ions from the acid react with hydroxide ions from the base to form water molecules. Heat energy is liberated in the process. A sample calculation on enthalpy is shown below:
The temperature of hydrochloric acid, T1= 22.5°C
Temperature of sodium hydroxide solution, T2= 22.5°C
Average temperature of the acid and alkali
T3 = = = 22.5°C
The highest temperature of the mixture T4 = 35.5CC
Temperature change ∆T = T4 — T3 = 35.5 — 22.5 = 13.0°C
The specific heat capacity of the solution = 4.2 KJ Kg-1 K-1. If in the experiment, 50 cm3 of 2M hydrochloric acid are neutralised by 50 cm3 of 2M sodium hydroxide, then the final volume of the resulting solution
= 50 + 50 = 100 cm3
If the density of the resulting solution is taken to be I g cm-3 then:
The mass of the solution = 100 cm3 X 1 g cm-3 = 100 g
Heat evolved = MC∆T
= 0.1 Kg X 4200 J Kg K-1 X 13.0 K = 5460 J
= 5.46 KJ
Moles of hydrochloric acid used = = 0.1 mol
Moles of H+ ions = 0. 1 mol
Moles of sodium hydroxide used = = 0.1 mol
Moles of 0H– ions = 0.1 mol
The equation of the reaction is
H+(aq) + OH–(aq) → H2O(l)
Thus 1 mol of H+ reacts with 1 mol of OH– to form 1 mol of water.
In the reaction between the acid and the base, 0.1 mol of water are formed.
When 0.1 mol of water are formed, 5.46 KJ of heat energy is evolved. Therefore, when 1 mol of water is formed
= 54.6 KJ of heat is evolved.
This is the molar heat of neutralisation of hydrochloric acid by sodium hydroxide. Molar heat of neutralisation: is the enthalpy change that takes place when one mole of hydrogen ions from an acid is completely neutralised by an alkali.
The enthalpy change can be incorporated in the neutralisation equation as follows:
H+(aq) + OH–(aq) → H2O(l) ∆Hneut = —54.6 KJ mol-1
Standard Conditions for Measuring Enthalpy Changes
The following are the standard conditions for measuring enthalpy changes:
- Temperature; 25°C (298K)
- Pressure; one atmosphere pressure (101.321 kPa).
Values of enthalpy changes measured under these conditions are called standard enthalpy changes. They are usually given a special symbol; ∆Hθ. A subscript is also added to the symbol to indicate type of enthalpy change involved. Thus:
- ∆Hθf refers to the standard molar enthalpy change of formation e.g
H2(aq) + O2(aq) → H2O(l) ∆Hθf (H2O) = —286 KJ mol-1
- ∆Hθc refers to the standard molar enthalpy change of combustion e.g
CH4 (g) + 2O2(g) → 2C02(g) + 2H2O(l) ∆Hθc (CH4) = —890 KJ mol-1
- ∆Hθneut refers to the standard molar cnthalpy change of neutralisation e.g
HCl(aq) + NaOH(aq) → NaCl(aq) + 2H2O(l) ∆Hθneut = —58 KJ mol-1
- ∆Hθsoln refers to the standard molar enthalpy change of dissolution (solution)
NaNO3 (s) + aq → NaNO3 (aq) ∆Hθsoln(NaNO3) = +21 KJ mol-1
- ∆Hθhyd means the standard molar enthalpy change of hydration e.g
Na+(s) + Cl–(s) + aq → Na+(aq) + Cl–(aq) ∆Hθhyd(NaCl) = –774 KJ mol-1
- ∆HθLatt refers to the standard molar enthalpy change of lattice formation
Na+(g) + Cl–(g) → NaCl(s) ∆HθLatt(NaCl) = –774 KJ mol-1
- ∆Hθat means the standard molar enthalpy change of atomisation e.g
Na(s) → Na+(g) ∆Hθat(Na) = +108.4 KJ mol-1
Hess’s Law
Hess’s Law of Constant heat summation states that: The energy change in converting reactants to products is the same regardless of the route by which the chemical change occurs.
The following diagram is an illustration of an energy cycle diagram that can be used to theoretically determine the enthalpy of formation of methane from the enthalpy of combustion of carbon and the enthalpy of combustion of methane.
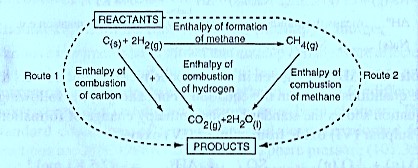
Using the energy cycle above it’s observed that whether route 1 or route 2 is followed, the end product is the same. This means that the energy changes for route 1are equal to the energy changes for route 2. This must be so because of the Law of conservation of energy. The enthalpy of formation of methane can be then calculated from the expression.
= +—
= — 393 + (—286 X 2 ) — (— 890 )
= — 75 KJ mol-1
Example 1
(a) Write down a balanced equation for the combustion of:
(i) Carbon (graphite)
(ii) Carbon (II) oxide
(b) Draw: (i) An energy level diagram for the formation of carbon (IV) oxide.
(ii) An energy cycle diagram incorporating the enthalpy of formation of carbon (IV) oxide.
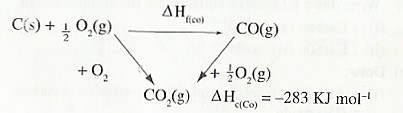
(c) Using your answers to (b), determine the enthalpy formation of carbon (II) oxide given that:
(I) Enthalpy of combustion of carbon =—393 KJ mol-1
(ii) Enthalpy of combustion of carbon (II) oxide = —283 KJ mol-1
Solution
- The thermochemical equations for the combustion of carbon and carbon (II) oxide are:
C(s) + O2(g) → CO2(g) ∆H = —393 KJ mol-1
CO(g) + O2(g) → CO2(g) ∆H = —283 KJ mol-1
The energy level diagram for the same reaction

From the energy cycle and energy level diagrams, the enthalpy of formation of carbon (II) oxide would be given by:
= —
∆Hθf (CO) = ∆Hθc (C) — ∆Hθc (CO)
= (— 393) — (—283 )
= — 110 KJ mol-1
Example 2
(a) Draw an energy cycle diagram linking the enthalpy formation of ethanol with its enthalpy of combustion and the enthalpy of combustion of its constituent elements.
(b) Calculate the enthalpy of formation of ethanol given that;
CH3CH2OH(l) + 3O2(g) → 2C02(g) + H2O(l) ∆H = —1260 KJ mol-1
H2 (g) + O2(g) → H2O(l) ∆H = —286 KJ mol-1
C (s) + O2(g) → C02(g) ∆H = —393 KJ mol-1
Solution
The energy cycle diagram for the formation and combustion ethanol is:

From the energy level diagram:
= +—
∆Hθf (C2H5OH) = 2 ∆HθC (C) + 3 ∆HθC(CO) — ∆HθC(C2H5OH)
= 2 X (— 393) + 3 X (—286 ) — (—1368 )
= — 786 + (—858 ) — (—1368 )
= —1644 + 1368
= — 276 KJ mol-1
Relationship between Heat of solution, Hydration and Lattice energy
Lattice energy: is defined as the energy change when one mole of an ionic compound is formed from its constituent ions in the gaseous state.
When Dissolving an ionic solid, first there is interaction of water molecules with the ions in the solid to such an extent that the solid dissociates into monatomic gaseous ions which scatter all directions in water. Therefore energy equivalent to the lattice energy is absorbed. This is the opposite of the process through which the ionic solid was formed. E.g. when sodium chloride is dissolved in water, the ionic bonds are first broken to release the gaseous ions.
NaCI(s) → Na+(g) + Cl–(g) ∆Hθ = +781 KJ mol-1
Secondly, the ions then get attracted to the polar water molecule and become hydrated i.e surrounded by water molecules.
The hydration process involves the formation of new bonds between the polar water molecules and the ions. The process is ways exothermic. The energy given out is known as hydration energy.
Na+(g) + aq → Na+(aq) ∆Hθ = —390 KJ mol-1
Cl– (g) + aq → Cl–(aq) ∆Hθ = —384 KJ mol-1
Hydration energy is defined as the energy change when one mole of gaseous ions becomes hydrated.
The overall enthalpy change of solution depends on whether the endothermic or the exothermic process is the larger. For sodium chloride, the endothermic process is greater than the exothermic process. Therefore the enthalpy of solution of sodium chloride has a positive value.
The following energy cycle diagram can be used to calculate the heat of solution of sodium chloride.
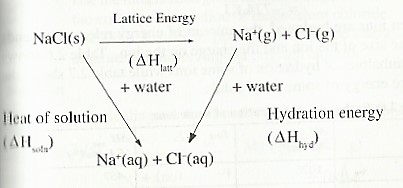
Or using an energy level diagram it can be shown as;
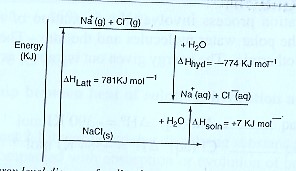
From the energy cycle or energy level diagram,
Heat of solution = Lattice energy + hydration energy
∆Hθsoln = ∆HθLatt — ∆Hθhyd
= 781 + (—774)
= +7 KJ mol-1
NOTE:
- The lattice energy is given a positive value in calculation above because bond breaking is an endothermic process.
- The hydration energy for sodium is the sum of the separate hydration energies of sodium ions and chloride ions i.e
∆Hhyd(NaCl) = ∆Hhyd(Na+) + ∆Hhyd(Cl–)
= —390 +(—384)
= —774 KJ mol-1
Fuels
Fuel is a substance that produces useful energy when it undergoes a chemical or nuclear reaction.
Fuels can be solids such as nuclear fuel, coke, coal, charcoal, and wood. Other fuels are liquids such as petrol, kerosene and diesel oil; or gases Like natural gas, biogas, water gas, and liquid petroleum gas.
Heating Values of Fuels
The heating value of a fuel: is, therefore, the amount of heat energy given out when a unit mass or a unit volume of fuel (in case the fuel is a gas) is completely burned in oxygen.
Heating value has the units KJ g-1 (Kilojoules per gram). It obtained by dividing the molar enthalpy of combustion by the formula mass of the fuel. For example, ethanol has an enthalpy of combustion of — I 360 KJ/mol. On dividing this by the formula mass of ethanol, 46, we get the heating value of ethanol as 30 KJ/g.
The Heating values for some other fuels are given in the table below;
Fuels |
Heating value in KJ/g |
Solid Fuels
Charcoal Coal Wood |
33
29 17 |
Liquid Fuels
Ethanol Fuel Oil Paraffin |
30
45 48 |
Gaseous Fuels
Methane (natural gas) Propane Butane |
55
50 48 |
Factors to consider when choosing a fuel
- Heating value
- Ease and rate of combustion
- Availability
- Ease of transportation
- Ease of storage
- Environmental effects
- Cost.
For example, wood and charcoal are chosen for domestic heating because:
- They are cheap
- They are readily available
- They can be easily transported
- When they burn they do not produce poisonous products
- They burn slowly.
Methylhydrazine (CH3NHNH2) is used for rocket propulsion because:
- It burns very rapidly producing large amounts of gases, in turn, creates a huge thrust as they escape.
- It has a very high heat of combustion (— 4740 KJ mol-1).
- It ignites easily.
Precautions necessary when using fuels
- Improper handling of fuels can result in death and destruction property. Each type of fuel should be handled with the necessary care and precautions:
- Charcoal stoves should be operated in well ventilated rooms avoid poisoning by carbon (II) oxide.
- Vehicle engines should not be left running in closed garages to avoid poisoning by carbon (II) oxide.
- Gas cylinders should be stored in well ventilated rooms far from heat sources. Only certified cylinders should be used for gas transport.
- Fuel storage facilities should be located far away from populated areas.
- People should keep off from spilled fuel from tankers.
Environmental Effects of Fuels
Fossil fuels such as coal and petroleum contain carbon, nitrogen and sulphur compounds which on burning produce poisonous gases such as sulphur (IV) oxide, sulphur (VI) oxide, carbon (II) oxide and nitrogen (IV) oxide.
The sulphur and nitrogen oxides dissolve in rain-water to produce acid rain which:
- Wears limestone buildings and statues.
- Corrodes iron sheets, iron gates, and other metallic structures.
- Acidifies lakes leading to death of plants and animals in these lakes.
- Leaches nutrients from plant leaves leading to their death.
- Leaches minerals from the soil leading to poor agricultural soils and low yields.
Carbon (IV) oxide and unburnt hydrocarbons from fuels contribute to global warming.
Tetracethyllead is added to petrol to prevent engine-flock. Petrol containing tetraethyllead burns to produce lead oxides which have been associated with nervous disorders and learning disabilities ii children.
Measures that are being taken to reduce pollution.
- Designing vehicles which use solar energy or electrical energy which are pollution-free.
- Fitting catalytic converters to the exhaust systems. Thes catalytic converters convert nitrogen oxides to harmless nitrogen, carbon (II) oxide to carbon (IV) oxide, unburnt hydrocarbons to water and catbon (IV) oxide.
- Designing engines which use unleaded petrol.
- Electronically controlling the quantity of air mixed with fuel to ensure more complete combustion.
- Adding fuels which contain oxygen in their molecules to petrol.
- Encourage other means of transport such as use of bicycles, electric trains.
- Use of heat exchangers to control heat from certain industrial processes.
Revision Exercise